GitHub

Problem Outline

Verification checks if the input-output relationships of a function, specifically deep neural networks (DNN) $\mathcal{F}$ in this case, hold. For an input specification imposed by a set $\mathcal{X}\subseteq \mathcal{D}_x$, we would like to check if the corresponding output of the function is contained in an output specification imposed by a set $\mathcal{Y}\subseteq \mathcal{D}_y$:

\[x\in\mathcal{X} \Longrightarrow y = \mathcal{F}(x) \in \mathcal{Y}.\]

Thus, a DNN-Verification problem consists of two main components:

  • model (DNN) : $\mathcal{F}$
  • safety property (input-output specification) : $\mathcal{X}, \mathcal{Y}$.

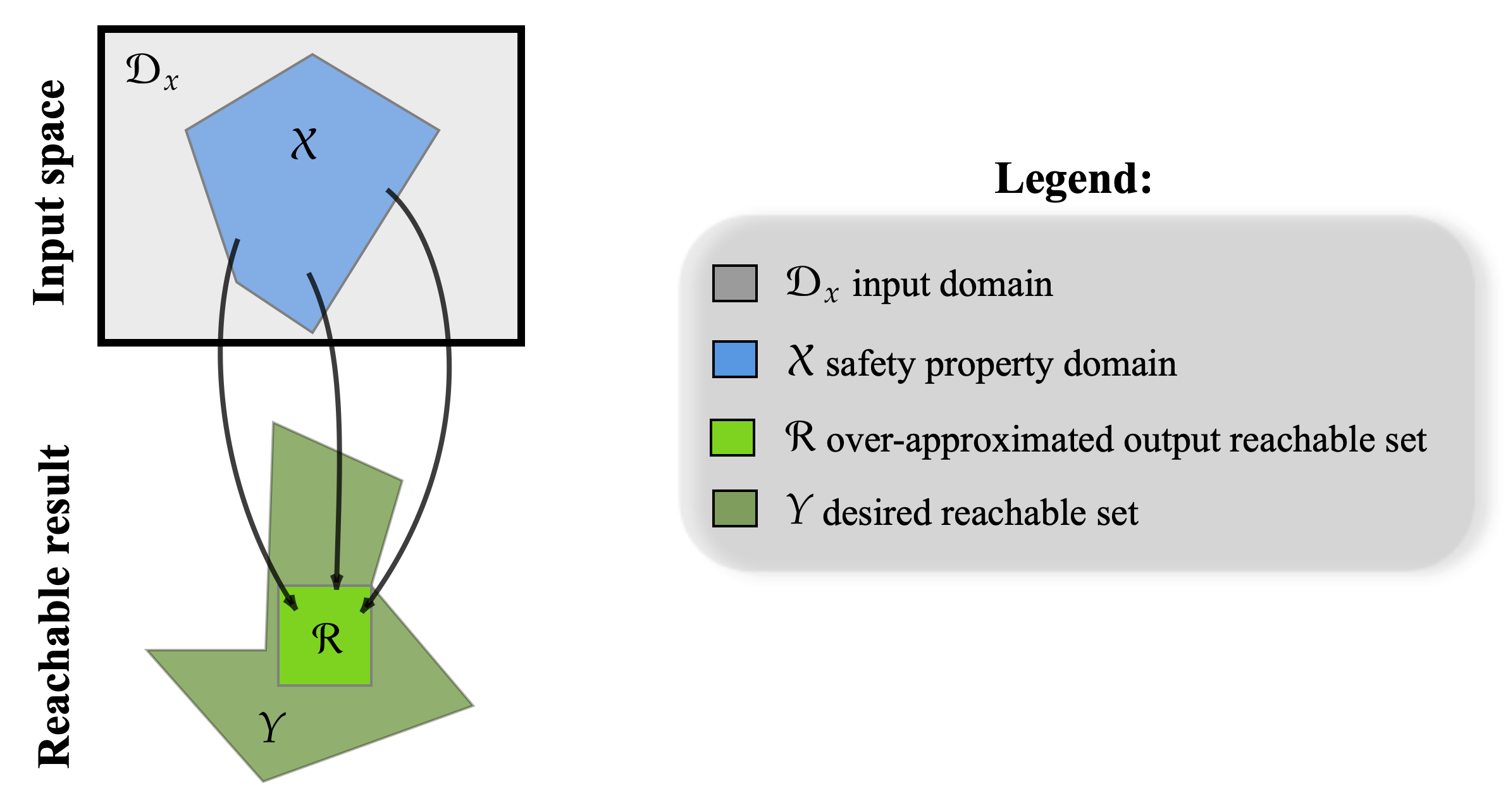
Due to the nonlinear and nonconvex nature of DNNs, estimating the exact reachable set is impractical, although there are algorithms that allow us to do this such as ExactReach. Thus, we preform an over-approximation of the reachable set, called $\mathcal{R}$. We check its containment in the desired reachable set $\mathcal{Y}$ which if ture, we can assert that the safety property holds.

Below, we give a brief overview of models (Network), safety property, and outputs (verification results).

Network

Details on Network

Safety Property

Details on Input-Output Specification

Output (Verification Results)

The following are the different result types used internally in the toolbox. We outline them here so that the user can have a better idea of what kind of conclusion the toolbox makes.

The user has to only interact with the wrapper ResultInfo, which contains the status and any other additional information needed to help understand the verification result.

Output resultExplanation
[BasicResult::holds]The input-output constraint is always satisfied.
[BasicResult::violated]The input-output constraint is violated, i.e., it exists a single point in the input constraint that violates the property.
[BasicResult::unknown]Could not be determined if the property holds due to timeout in the computation.
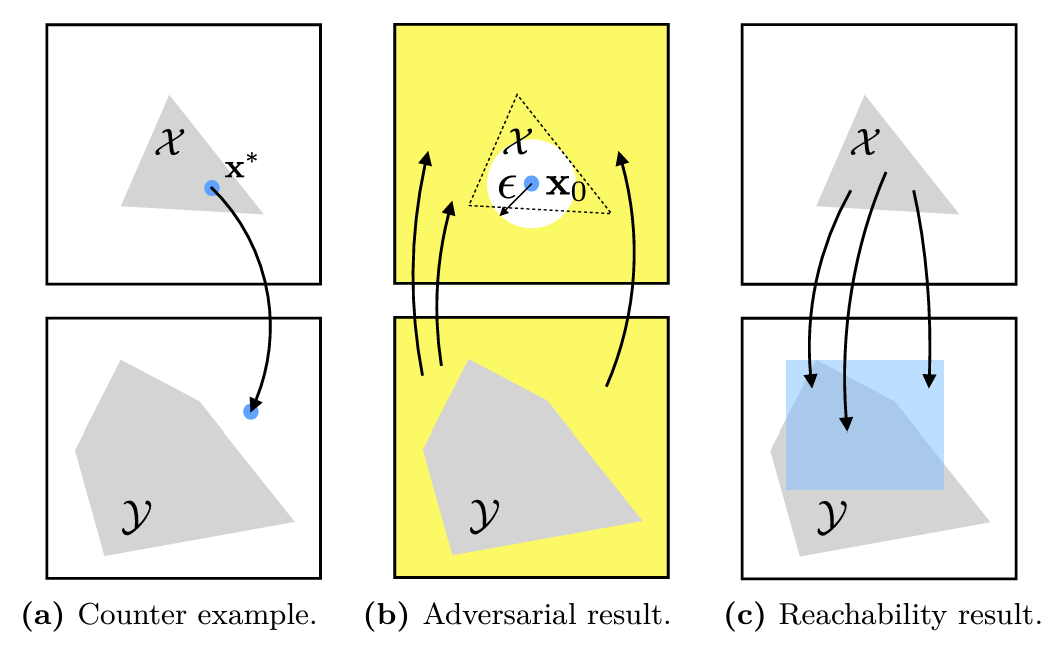
[CounterExampleResult]Like BasicResult, but also returns a counterexample if one is found (if status = :violated). The counterexample is a point in the input set that, after the NN, lies outside the output constraint set.
[AdversarialResult]Like BasicResult, but also returns the maximum allowable disturbance in the input (if status = :violated).
[ReachabilityResult]Like BasicResult, but also returns the output reachable set given the input constraint (if status = :violated).
[EnumerationResult]Set of all the (un)safe regions in the safety property's domain.

Problem

ModelVerification.Problem — Type
Problem{P, Q}(network::Network, input::P, output::Q)

Problem definition for neural verification. The verification problem consists of: for all points in the input set, the corresponding output of the network must belong to the output set.

There are three ways to construct a Problem:

  1. Problem(path::String, model::Chain, input_data, output_data) if both the .onnx model path and Flux_model are given.
  2. Problem(path::String, input_data, output_data) if only the .onnx model path is given.
  3. Problem(model::Chain, input_data, output_data) if only the Flux_model is given.

Fields

  • network : Network that can be constructed either using the path to an onnx model or a Flux.Chain structure.
  • input : Input specification defined using a LazySet.
  • output : Output specification defined using a LazySet.
source
ModelVerification.prepare_problem — Method
prepare_problem(search_method::SearchMethod, split_method::SplitMethod, 
                prop_method::PropMethod, problem::Problem)

Converts the given Problem into a form that is compatible with the verification process of the toolbox. In particular, it retrieves information about the ONNX model to be verified and stores them into a Model. It returns the Problem itself and the Model structure.

Arguments

  • search_method (SearchMethod): Search method for the verification process.
  • split_method (SplitMethod): Split method for the verification process.
  • prop_method (PropMethod): Propagation method for the verification process.
  • problem (Problem): Problem definition for model verification.

Returns

  • model_info (Model): Information about the model to be verified.
  • problem (Problem): The given problem definition for model verification.
source

Result

ModelVerification.ResultInfo — Type
ResultInfo(status, info)

Like BasicResult, but also returns a info dictionary that contains other informations. This is designed to be the general result type.

Fields

  • status (Symbol): Status of the result, can be :holds, :violated, or :unknown.
  • info (Dict): A dictionary that contains information related to the result, such as the verified bounds, adversarial input bounds, counter example, etc.
source
ModelVerification.BasicResult — Type
BasicResult(status)

Result type that captures whether the input-output constraint is satisfied. Possible status values:

:holds (io constraint is satisfied always)

:violated (io constraint is violated)

:unknown (could not be determined)

Fields

  • status (Symbol): Status of the result, can be :holds, :violated, or :unknown.
source
ModelVerification.CounterExampleResult — Type
CounterExampleResult(status, counter_example)

Like BasicResult, but also returns a counter_example if one is found (if status = :violated). The counter_example is a point in the input set that, after the NN, lies outside the output set.

source
ModelVerification.validate_status — Function
validate_status(st)

Validates the status code. Only (:holds, :violated, :unknown) are accepted.

Arguments

  • st (Symbol): Status code.

Returns

  • Assertion Error if the given st is not one of (:holds, :violated, :unknown).
  • Otherwise, returns the given st.
source