Input-Output Specification

Input-Output Specification

Safety Property

A safety property is essentially an input-output relationship for the model we want to verify. In general, the constraints for the input set $\mathcal{X}$ and the output set $\mathcal{Y}$ can have any geometry. For the sake of simplicity, ModelVerification.jl uses convex polytopes and the complement of a polytope to encode the input and output specifications. Specifically, our implementation utilizes the geometric definitions of LazySets, a Julia package for calculus with convex sets. The following section dives into the geometric representations ModelVerification.jl uses and the representations required for each solver.

Geometric Representation

Different solvers implemented in ModelVerification.jl require the input-output specification formulated with particular geometries. We report here a brief overview of the sets we use. For specifics, please read Algorithms for Verifying Deep Neural Networks by C. Liu, et al. and Sets in LazySets.jl.

HR = Hyperrectangle
HS = HalfSpace
HP = HPolytope
SS = StarSet
IS = ImageStar
ZT = Zonotope
PC = PolytopeComplement
CH = ConvexHull

Solver	Input set	Output
Ai2	`ZT,SS,HP,HR`	`ReachabilityResult`, `CounterExampleResult`
CROWN	`ZT,SS,HP,HR,CH`	`BasicResult`
$\alpha$-CROWN	`ZT,SS,HP,HR,CH`	`BasicResult`
$\beta$-CROWN	`ZT,SS,HP,HR,CH`	`BasicResult`
$\alpha$-$\beta$-CROWN	`ZT,SS,HP,HR,CH`	`BasicResult`
ImageZono	`CH`	`ReachabilityResult`, `CounterExampleResult`
ImageStar	`CH`	`ReachabilityResult`, `CounterExampleResult`

Hyperrectangle (`Hyperrectangle`)

Corresponds to a high-dimensional rectangle, defined by

\[|x-c| \le r,\]

where $c\in\mathbb{R}^{k_0}$ is the center of the hyperrectangle and $r\in\mathbb{R}^{k_0}$ is the radius of the hyperrectangle.

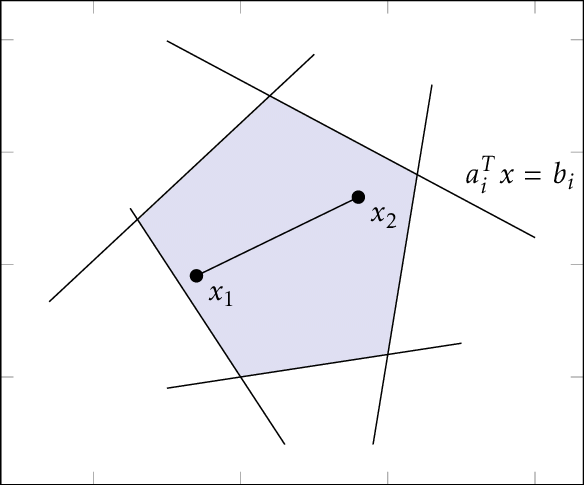
HalfSpace (`HalfSpace`)

Represented by a single linear inequality constraint

\[a^\top x \le b,\]

where $a\in\mathbb{R}^{k_0}$ and $b\in\mathbb{R}$.

Halfspace-Polytope (`HPolytope`)

HPolytope uses a set of linear inequality constraints to represent a convex polytope, i.e., it is a bounded set defined using an intersection of half-spaces.

\[Ax \le b,\]

where $A\in\mathbb{R}^{k\times k_0}, b\in\mathbb{R}^k$ with $k$ representing the number of inequality constraints.

StarSet (`Star`)

Only convex star set is considered in this toolbox. A convex star set is an affine transformation of an arbitrary convex polytope,

\[x = c + \begin{bmatrix} r_1 & r_2 & \cdots & r_l \end{bmatrix} \alpha,\; C\alpha \le d,\]

where $c\in\mathbb{R}^{k_0}$ is the center of the star set, $r_i\in\mathbb{R}^{k_0},\; i\in\{1,\dots,l\}$ are generators of the star set, $C\in\mathbb{R}^{k\times l}$, $d\in\mathbb{R}^{k}$, $\alpha\in\mathbb{R}^l$ is the free parameter that belongs to a unit hypercube, and $k$ is the number of inequality constraints on $\alpha$. $l$ is the degree of freedom of the star set.

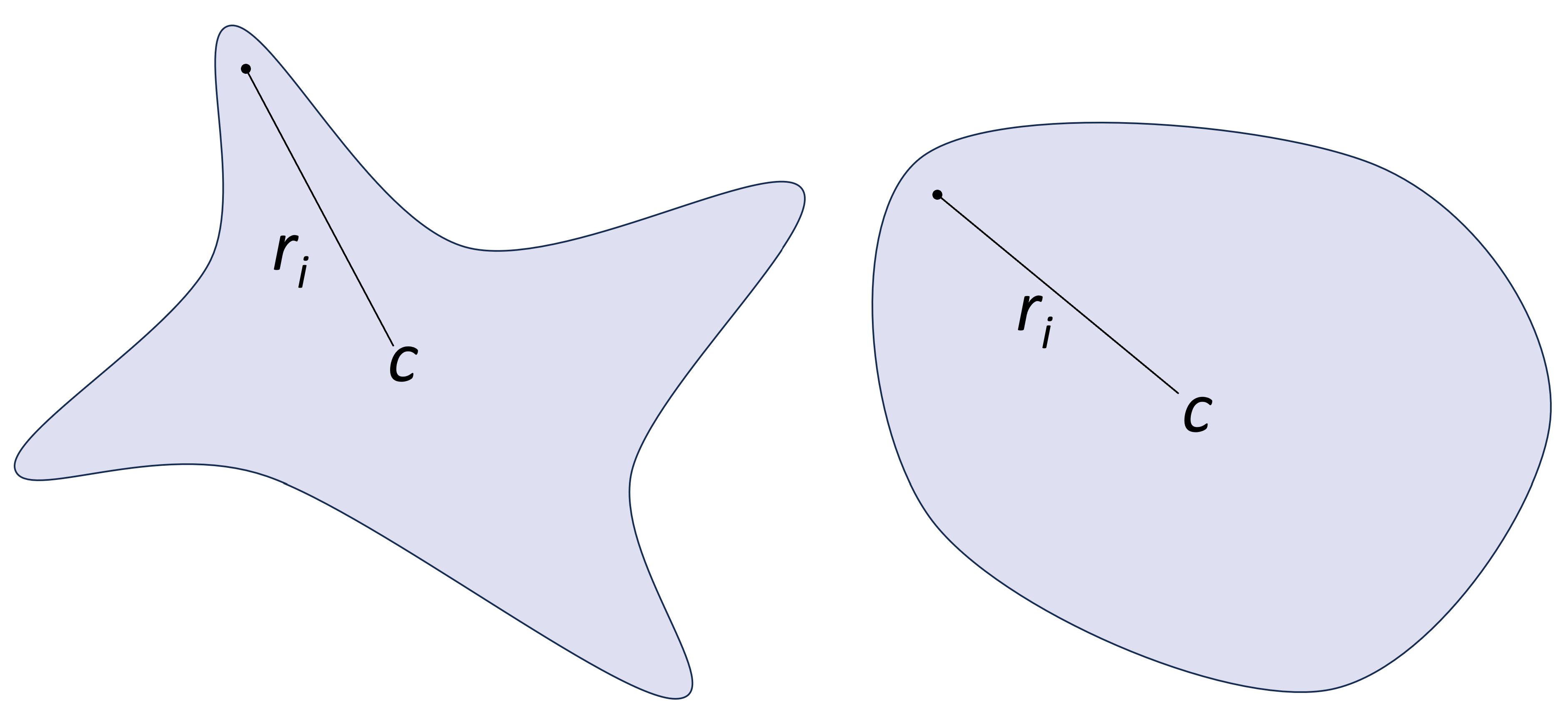The general starset, on the left, is not necessarily convex. We only consider convex starsets.

Zonotope (`Zonotope`)

Zonotope is basically as star set in which all predicate variables are in the range of $[-1, 1]$. Zonotope represents polytopes that can be written as affine transformations of a unit hypercube, defined as

\[x = c + \begin{bmatrix} r_1 & r_2 & \cdots & r_l \end{bmatrix} \alpha,\; |\alpha| \le 1,\]

where $c\in\mathbb{R}^{k_0}$ is the center of the zonotope, $r_i\in\mathbb{R}^{k_0},\; i\in\{1,\dots,l\}$ are generators of the zonotope, and $\alpha\in\mathbb{R}^l$ is the free parameter that belongs to a unit hypercube. $l$ is the degree of freedom of the zonotope.

ImageStar

ImageStar is an extension of the star set where the center and generators are images with multiple channels.

\[x = c + \begin{bmatrix} r_1 & r_2 & \cdots & r_l \end{bmatrix} \alpha,\; C\alpha \le d,\]

where $c\in\mathbb{R}^{h\times w \times k_0}$ is the center image, $r_i\in\mathbb{R}^{h \times w \times k_0},\; i\in\{1,\dots,l\}$ are the generator iamges, $C\in\mathbb{R}^{k\times l}$, $d\in\mathbb{R}^{k}$, and $h,w,k$ are the height, width, and number of channels (input dimension) of the images respectively. $\alpha\in\mathbb{R}^l$ is the free parameter that belongs to a unit hypercube, and $k$ is the number of inequality constraints on $\alpha$. $l$ is the degree of freedom of the star set.

ImageZono

ImageZono is an extension of the zonotope where the center and generators are images with multiple channels.

\[x = c + \begin{bmatrix} r_1 & r_2 & \cdots & r_l \end{bmatrix} \alpha\]

where $c\in\mathbb{R}^{h\times w \times k_0}$ is the center image, $r_i\in\mathbb{R}^{h \times w \times k_0},\; i\in\{1,\dots,l\}$ are the generator iamges, and $h,w,k$ are the height, width, and number of channels (input dimension) of the images respectively. $\alpha\in\mathbb{R}^l$ is the free parameter that belongs to a unit hypercube and $l$ is the degree of freedom of the zonotope.

PolytopeComplement (`Complement`)

PolytopeComplement is a type that represents the complement of a polytope, that is the set

\[Y = X^c = \{ y\in\mathbb{R}^n : y \notin X \}.\]

References

[1] C. Liu, T. Arnon, C. Lazarus, C. Strong, C. Barret, and M. J. Kochenderfer, "Algorithms for Verifying Deep Neural Networks," in Foundations and Trends in Optimization, 2021.

[2] T. Gehr, M. Mirman, D. Drashsler-Cohen, P. Tsankov, S. Chaudhuri, and M. Vechev, "Ai2: Safety and Robustness Certification of Neural Networks with Abstract Interpretation," in 2018 IEEE Symposium on Security and Privacy (SP), 2018.

[3] M. Forets and C. Schilling, "LazySets.jl: Scalable Symbolic-Numeric Set Computations," in Proceeds of the JuliaCon Conferences, 2021.

[4] HD. Tran, S. Bak, W. Xiang, and T.T. Johnson, "Verification of Deep Convolutional Neural Networks Using ImageStars," in Computer Aided Verification (CAV), 2020.

`Spec`

Specifications

ModelVerification.Spec — Type

Spec

Abstract super-type for input-output specifications.

Hyperrectangle (Hyperrectangle)

HalfSpace (HalfSpace)

Halfspace-Polytope (HPolytope)

StarSet (Star)

Zonotope (Zonotope)